Investigating the effects of non-uniform input data windowing on electrical load disaggregation performance
Non-intrusive Load Monitoring (NILM) is an application of smart meters to decompose the aggregated electrical load consumption into individual appliance profiles. State-of-the-art NILM methods based on neural networks showed remarkable disaggregation accuracy results. Internally, the network input data are sampled based on a windowing technique with a fixed window length limiting the number of input data, affecting the disaggregation performance. In addition, the use of different window length configurations per device increases the complexity of the model.
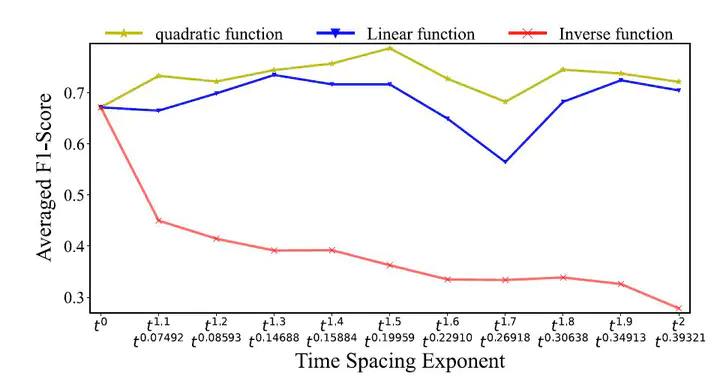
In this project, a windowing method is proposed using nonlinear algebraic functions to capture the input data points. The goal is to investigate the effect of expanding the time interval of the input window on load disaggregation without influencing the model complexity. Non-equidistant temporal sampling technique splits the traditional window into two sequences according to a fraction: a high-resolution sequence and an non-equally spaced sequence generated by means of non-linear algebraic functions, allowing the input window to contain more historical information without having to adjust the window length parameter. For evaluating the proposed technique, different variants of non-equidistant temporal sampling are suggested, the inverse and the linear downsampling function. The inverse generates an entirely non-equally spaced window, and the linear function creates a fraction of the window with equally time-spaced samples. Both functions cover the same effective window length as the proposed method.
The results confirm a positive impact of aggregating the historical information on load disaggregation. The promising potential of the proposed technique shown during the evaluation can make a step forward in the NILM field, as collecting historical input data according to a non-equidistant or linear manner ensure an improvement in the performance without affecting the model complexity.